Note de l’observatoire de macroéconomie n°2022-02

Avec 34% de son pétrole, 55% de son gaz et 26% de son charbon venant de Russie, l’Allemagne s’est trouvée au centre du débat sur l’opportunité de mettre en place un embargo sur l’énergie russe en Europe. Face à la résistance de son gouvernement à suivre cette voie, Bachmann et al. (2022) ont quantifié les effets sur l’économie allemande d’un arrêt des importations d’énergie en provenance de Russie. Ce débat concernant tous les pays de l’Union Européenne qui seraient aussi impactés, nous évaluons le coût de cet embargo pour l’économie mondiale, et en particulier pour les pays de l’Union Européenne. Malgré la complexité d’une telle évaluation, et la prudence avec laquelle il faut interpréter les résultats, il est nécessaire d’estimer les coûts de cet embargo pour informer les citoyens de l’Union Européenne et mettre en place de politiques d’accompagnement si cette politique est adoptée. L’intérêt de la contribution de Bachmann et al. (2022) est d’apporter des résultats pour l’Allemagne mais également pour les principales économies, même s’ils ne sont pas directement présentés dans leur étude. Nous les analysons dans cette note pour évaluer le coût de l’embargo sur les énergies russes pour les économies européennes. Les principales conclusions sont : 

1. Le coût moyen de l’embargo dans l’Union Européenne équivaut à une réduction de -0,7% des dépenses nationales (consommation des ménages, investissement des entreprises et dépenses publiques) par an et par habitant. 
2. Le coût de l’embargo serait plus élevé pour la Russie que pour l’Union européenne avec une perte de -2,3% des dépenses nationales. 
3. Il existe une forte hétérogénéité dans les coûts de l’embargo au sein de l’Union Européenne entre la Lituanie (le pays le plus impacté avec -5,3% des dépenses nationales) et le Luxembourg (qui connaîtrait un gain de 0,2% des dépenses nationales). L’Allemagne et la France occupent une position intermédiaire dans l’Union Européenne avec des pertes de -0,3% et -0,2% des dépenses nationales respectivement. 
4. Au sein de chaque pays, il existe d’importantes différences sectorielles avec une plus forte contraction des secteurs plus dépendants de l’énergie.

François Langot, Professeur à l’Université du Mans et directeur de l’Observatoire de Macroéconomie flangot@univ-lemans.fr

Fabien Tripier, Professeur à l’Université Paris Dauphine – PSL et économiste à l’Observatoire de Macroéconomie fabien.tripier@dauphine.psl.eu

Les premières sanctions à l’encontre de la Russie ont été une réaction forte suite à l’invasion de l’Ukraine. L’évolution du conflit amène les pays de de l’Union Européenne (UE) à envisager un embargo sur les importations d’énergie (gaz, pétrole et charbon) de Russie. De nombreux commentateurs freinent cette proposition en arguant que ces sanctions induiraient des pertes insupportables pour les populations de l’UE. Connaît-on vraiment l’ampleur de ces pertes ?

Un groupe d’économistes¹ a évalué le coût de cet embargo pour l’Allemagne. Leurs estimations conduisent à une réduction des dépenses de consommation annuelle d’un allemand allant de 80 à 1000€. Cette analyse doit être appliquée à d’autres pays, car c’est ensemble que les pays de l’UE devront décider de s’engager dans cet embargo, en concertation avec nos autres partenaires. Nous analysons dans cette note les résultats pour l’économie internationale qui ne sont pas directement présentés dans Bachmann et al. (2022)².

1. Les apports d’une évaluation en équilibre général

Le coût de l’embargo est perçu comme très élevé car il n’y aurait pas substitution possible aux sources d’énergie russe, et en premier lieu aucune possibilité d’y substituer de l’énergie d’autres pays producteurs. En effet, si l’on se place du côté des entreprises, et dans le cas extrême où aucune adaptation de la chaîne de production n’est possible (substitution nulle entre les facteurs de production, i.e. une fonction de production dite à la  Léontief), la perte de production est égale à la baisse d’énergie. Pour l’Allemagne, une réduction de -30% de sa consommation d’énergie (ce qui correspond aux importations énergétiques allemandes venant de Russie) réduirait son PIB de -30%, ce qui est considérable.

Or, même un très faible de degré de substitution peut fortement réduire ce coût, même dans le cas où l’énergie russe n’est pas remplacée par une énergie venant d’un autre pays. En effet, prendre en compte une possibilité de substituer, même très faible, modifie ce scenario. En faisant passer l’élasticité de substitution de 0 (le cas précédent de la fonction de production Léontief) à 0,1, la réduction du PIB n’est plus que de -1,57% au lieu de -30% (voir encadré 2)³.

Le constat est le même, si l’on se place maintenant du côté du consommateur. Bachmann et al. (2022) montrent qu’une réduction de 30% de la consommation d’énergie ne réduirait les dépenses de consommation allemandes que de -1,5%, dans un scenario extrême où la part de l’énergie dans la consommation allemande passerait de 2.5% à 7.5% (triplement de la part) du fait d’une hausse considérable des prix de l’énergie induite par la réduction globale de l’offre d’énergie (voir l’illustration numérique de l’encadré 1). Ceci s’explique par le fait que l’on part d’une situation où la part de l’énergie dans les dépenses de consommation est relativement faible en Allemagne (2,5%). Ainsi, même si des tensions sur les prix peuvent faire croître considérablement la part de l’énergie dans la consommation allemande, les pertes induites par l’embargo sur l’énergie russe restent beaucoup plus faibles que la perte de 30% de PIB prédite par un raisonnement où aucune substitution ne serait possible.

Ces analyses présentent néanmoins plusieurs limites : (i) le prix de l’énergie est exogène, (ii) il n’est pas envisagé de recomposition sectorielle de l’économie et (iii) les liens internationaux par le commerce ne sont pas pris en compte, en particulier la possibilité d’importer de l’énergie venant d’autres pays. En effet, la difficulté de l’évaluation du coût économique de cet embargo est qu’un arrêt des importations d’énergie de Russie bouleverse la chaîne de production mondiale avec des effets en cascade spécifique à chaque pays, via h’hétérogénéité de leurs secteurs d’activité, dont celui de l’énergie, leurs relations commerciales et le prix mondial de l’énergie.

Le modèle développé par Baqaee et Fahri (2021)⁴, et utilisée dans Bachmann et al. (2022), est alors d’un immense secours. Basé sur les derniers développements de la macroéconomie internationale, ce modèle détermine les conditions (prix et contrats) pour lesquelles des individus (ménages et entreprises) acceptent de participer ou pas aux échanges marchants (consommation, travail, production de biens finaux et intermédiaires, exploitation et vente des ressources rares…) en fonction de règles établies par les États. Ce cadre est donc l’outil adéquat pour évaluer l’impact de la modification d’une règle (blocage des exportations d’énergie de la Russie vers l’UE) sur le pouvoir d’achat. Les interactions d’équilibre général, au niveau de la chaîne de production mondiale vont déterminer les modifications de prix de tous les facteurs de production qui vont alors modifier les comportements d’arbitrage sur les différents marchés en cherchant à remplacer les énergies russes.

Le modèle de Baqaee et Fahri (2021), décrit dans l’encadré 1, comprend 40 pays ainsi qu’un pays composite résumant le « reste du monde ». Au sein de chaque pays, les entreprises produisent avec des facteurs primaires, un type de travail par type de bien produit, et des biens intermédiaires, dont l’énergie. Ces biens intermédiaires sont produits par le tissu industriel de chaque pays, composé de 30 secteurs. Lorsqu’un producteur ou un ménage d’un pays achète des produits à une industrie, il consomme un « assemblage » de biens provenant des entreprises de l’ensemble des différents pays. L’hypothèse centrale de ce modèle est qu’il n’existe pas de contrainte quantitative stricte et donc que les prix peuvent s’ajuster suffisamment à la hausse pour signaler l’éventuelle rareté d’un bien.

Les possibilités de substitution sont centrales dans ce modèle car elles déterminent comment (i) les consommateurs peuvent substituer les biens entre eux, dont l’énergie, (ii) les entreprises peuvent substituer les biens intermédiaires entre eux, dont l’énergie, (iii) les entreprises peuvent substituer du travail aux biens intermédiaires, (iv) l’offre d’énergie va répondre à l’évolution des prix dans les différents pays.

Dans une perspective de très court terme, il est supposé dans la suite qu’il est très difficile de substituer ces énergies russes par d’autres inputs : l’élasticité de substitutions retenue est en effet trois fois plus faibles que les estimations reportées par Labandeira et al (2017) et Auffhammer et Rubin (2018). Ceci implique donc de fortes variations de prix et d’importants changements d’activités entre secteurs et entre pays.

Comme dans Bachmann et al. (2022), on suppose que l’UE met des barrières strictes contre toutes les importations en provenance de Russie (y compris l’énergie). Cette expérience est donc plus extrême qu’un arrêt des exportations russes d’énergie vers l’UE. Nous retenons cette stratégie car, en plus de l’énergie, les principales transactions avec le Russie sont aujourd’hui déjà bloquées (finance, agriculture, transports aériens,…). Cette modélisation va donc sur-estimer le coût d’un embargo à l’encontre des énergies russes. Mais la Russie n’est pas totalement isolée du commerce internationale, gardant ainsi la possibilité de vendre à d’autres partenaires en supportant de plus forts coûts.

2. Une sanction efficace et des pays européens différemment impactés

Nos simulations du modèle de Baqaee et Fahri (2021) reprenant les hypothèses de Bachmann et al. (2022) conduisent aux résultats suivants.

Le coût moyen de l’embargo dans l’UE équivaut à une réduction de -0,7% des dépenses nationales brutes (c’est-à-dire la somme de la consommation des ménages, de la consommation des administrations publiques et de la formation brute de capital fixe) par an et par habitant (DNB par la suite)⁵. Le coût de l’embargo serait plus élevé pour la Russie que pour l’UE avec une perte annuelle de -2,3% des DNB. Ces fortes pertes russes soulignent une forte dépendance aux exportations d’énergie et une faible capacités à compenser par d’autres activités ses pertes, même si l’accroissement du prix de l’énergie amortit ce choc pour la Russie. Même si les niveaux de ces pertes peuvent être discutés, cette évaluation montre déjà que le sanctionné, ici la Russie, perd plus de trois fois plus qu’un pays de l’UE.

Des structures sectorielles et des dépendances extérieures spécifiques à chaque pays impliquent de forts écarts de coûts de l’embargo au sein de l’UE (graphique 1). La Lituanie serait le pays le plus impacté (-5,3% des DNB) et le Luxembourg connaîtrait un gain (0,2% des DNB). L’Allemagne et la France occupent des positions intermédiaires (11^ième et 20^ième rang des pays européens les plus touchés) avec des pertes de -0,3% et -0,2% des DNB respectivement.

En utilisant les données de la Banque Mondiale⁶, il est possible d’exprimer ces variations en montant de dépenses annuelles par habitant. Pour un russe, le coût annuel de cet embargo s’établirait à 534€. Au sein de l’UE, chaque habitant verrait sa consommation baisser en moyenne de 227€ par an. Pour un ménage avec deux enfants, cela représente une perte de 908€ par an. La Lituanie verrait les consommation de chacun de ses habitants baisser de 1745€ par an. Viendraient ensuite, la Slovénie (716€), la Bulgarie (563€), la Finlande (440€), la Tchéquie (331€), l’Estonie (238€), la Lettonie (226€), la Hongrie (200€), Chypre (200€) et la Suède (153€). Un allemand perdrait 125€ par an et un français 54€. Il est intéressant de noter que, par le jeu des substitutions et réallocations d’activité, certains pays européens gagneraient à la mise en place de l’embargo comme le Luxembourg (110€), l’Irlande (37€) et le Danemark (12€). Ici encore, même si les niveaux de ces pertes peuvent être discutés, cette évaluation met l’accent sur l’hétérogénéité des pertes induites, un Lituanien perdant plus de 30 fois plus qu’un français. Remarquons que nos partenaires nord-américains seraient nettement moins impactés par cet embargo avec une perte annuelle de 16€ pour un américain et même un gain de 57€ pour un canadien.

Il est important de noter que ces évaluations changent peu lorsque les possibilités de substitution sont légèrement modifiées, tout en restant dans une perspective de court terme où l’adaptabilité de la chaîne de production mondiale reste très modérée⁷: par année, un lituanien perdrait entre 1700 et 1800€, un allemand entre 115 et 155€, un français entre 50 et 70€.

Comment expliquer ces résultats ? Tout d’abord, le modèle tient compte des possibles réallocations internationales : pour les énergies, le Canada peut vendre davantage d’électricité aux États-Unis, qui peuvent alors vendre plus de gaz à le France qui peut alors vendre plus d’électricité à l’Allemagne. Ensuite, des substitutions s’opèrent : spécifiquement à chaque pays, les ménages et les entreprises achètent moins de l’énergie devenue rare et chère, l’utilisant là où elle est la moins substituable. Le modèle tenant compte des spécialisations sectorielles et de la structure du commerce international de chaque pays, explique pourquoi les plus utilisateurs d’inputs russes (dont l’énergies) seront plus impactés. Enfin, certaines productions intenses en intrants russes (dont l’énergies) se délocalisent vers d’autres pays.

Bien entendu, cette approche a des limites. Premièrement, le gaz n’est pas un input particulier de la fonction de production, mais il entre dans le modèle via un secteur agrégé « Électricité, gaz et eau ». Or, en réalité, le gaz ne peut pas être remplacé par l’électricité dans de nombreux processus de production (par exemple dans l’industrie chimique). Deuxièmement, ce modèle fait abstraction de l’impact de potentielles contractions de court terme de la demande dues à des rigidités de prix, qui pourraient accroître la chute de l’activité. Troisièmement, ce modèle ne tient pas compte des coûts d’ajustement liés aux réallocations des facteurs entre les secteurs. Ces trois points suggèrent que nous sous-évaluons les coûts de l’embargo. En revanche, cette politique pourrait aussi avoir la vertu d’ accélérer la transition écologique européenne (voir Schumacher et al (2022)⁸). Des futures recherches intégrant ces quatre éléments affineront l’évaluation de ces coûts.

Ces montants peuvent paraître modestes au regard des résistances à la mise en place de cet embargo. Il faut d’abord garder à l’esprit que de grandes disparités internes existent au sein de chaque pays : en France, les secteurs des transports et de l’agriculture connaissent un fort déclin de -6% et -4%, respectivement (cf. Graphique 2). Le graphique 2 illustre également la réallocation d’activité entre les secteurs avec une progression du secteur de l’énergie domestique (comprenant l’énergie nucléaire) et de secteurs faiblement intensifs en énergie, comme le commerce⁹.

Ces évaluations mettent l’accent sur la capacité de l’économie mondiale à absorber, pour un coût raisonnable, un tel choc : les réallocations « assurent » les pays contre ce choc négatif d’offre localisé. Cela s’explique car nous considérons l’arrêt des transactions entre la Russie et l’UE d’un nombre limité de biens (gaz, pétrole, charbon). À titre d’illustration, l’exclusion complète de la France du commerce international conduirait chaque Français à réduire sa dépense de 11 550€ par an, soit une baisse de -30% (voir Baqaee et Farhi (2021)).

Pour faciliter une décision européenne concertée d’un embargo sur les énergies russes, un mécanisme de redistribution au sein de l’UE devrait être mis en place pour aider les pays les plus touchés, et ainsi répartir équitablement la contribution de chaque pays.

Graphique 1. Variation des dépenses nationales brutes suite à l’embargo sur les énergies russes

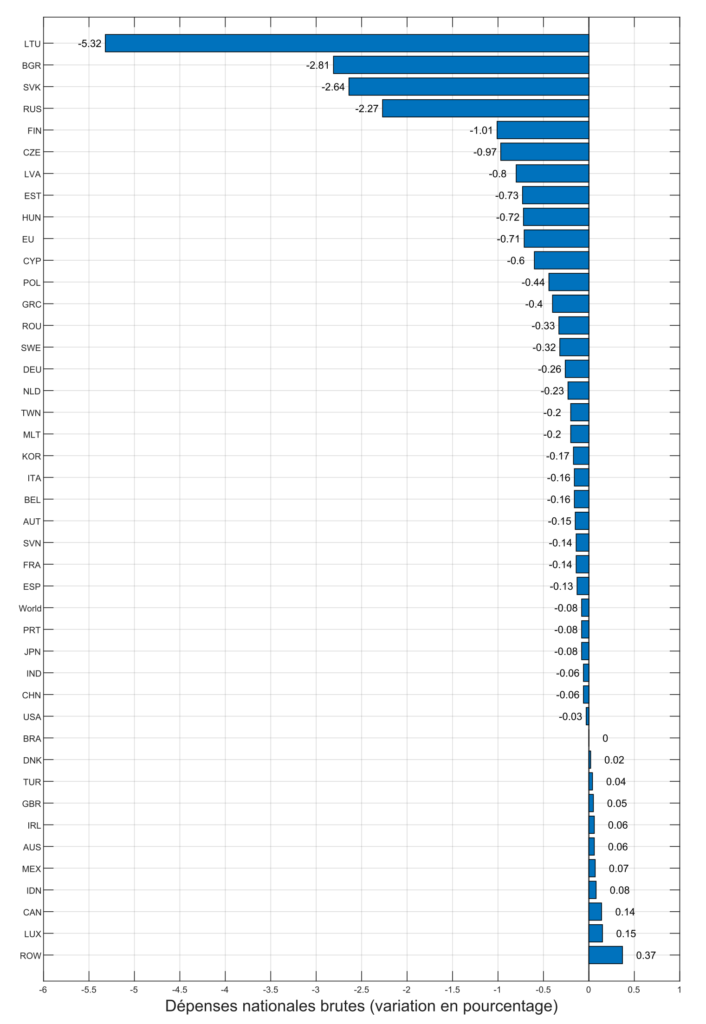
Source : simulation des auteurs du modèle de Baqaee and Farhi (2021) à partir des codes de réplication de Bachmann et al. (2022) téléchargés de https://benjaminmoll.com/RussianGas_Replication/
Pays : AUS Australie, AUT Autriche, BEL Belgique, BGR Bulgarie, BRA Brésil, CAN Canada, CHN Chine, CYP Chypre, CZE République tchèque, DEU Allemagne, DNK Danemark, ESP Espagne, EST Estonie, FIN Finlande, FRA France, GBR Royaume-Uni, GRC Grèce, HUN Hongrie, IDN Indonésie, IND Inde, IRL Irlande, ITA Italie, JPN Japon, KOR Corée, LTU Lituanie, LUX Luxembourg, LVA Lettonie, MEX Mexique, MLT Malte, NLD Pays-Bas, POL Pologne, PRT Portugal, ROU Roumanie, RUS Fédération de Russie, SVK République slovaque, SVN Slovénie, SWE Suède, TUR Turquie, TWN Taiwan, USA États-Unis, ROW Reste du monde, World Monde, EU, Union européenne. Données pour reproduire les figures (format Excel)

Graphique 2. Variation de l’activité par secteur suite à l’embargo sur les énergies russes pour la France

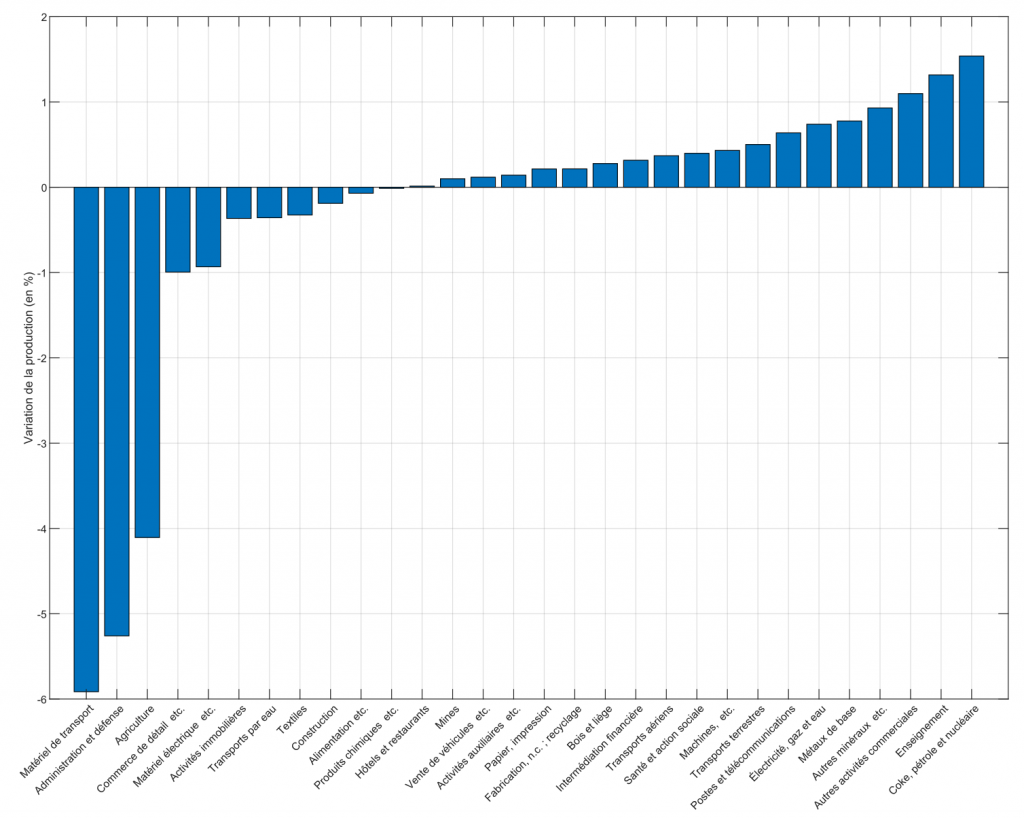
Source : simulation des auteurs du modèle de Baqaee and Farhi (2021) à partir des codes de réplication de Bachmann et al. (2022) téléchargés de https://benjaminmoll.com/RussianGas_Replication. Données pour reproduire les figures (format Excel)

Encadré 1 : Le modèle de commerce international sectoriel de Baqaee et Farhi (2021).

Le monde est constitué d’un ensemble de C pays, de N producteurs fabriquant différents biens et de F facteurs de production. Chaque producteur et chaque facteur de production est localisé dans un pays. Les producteurs et facteurs de production d’un pays c sont N_c et F_c. Les F_c facteurs situés dans le pays c peuvent appartenir à n’importe quel ménage, pas nécessairement un ménage du pays c. Le ménage représentatif du pays c a des préférences homothétiques

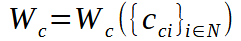
et fait face à la contrainte budgétaire suivante

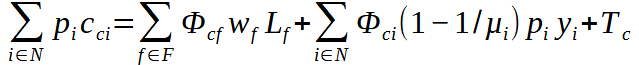
où c_ci est la quantité de bien i consommée par le ménage du pays c, w_f et L_f le salaire et la quantité de facteur f , p_i le prix et y_i la quantité de bien i, et T_c un transfert forfaitaire exogène. Le membre de droite est le revenu du pays c : la première somme est le revenu des facteurs primaires, la deuxième somme est le revenu des dividendes. Chaque élément Φ_ci de la matrice Φ, de dimension C × (N + F), donne la part de valeur ajoutée du bien i qui revient aux ménages du pays c et µ_i est le taux de marge sur les ventes.

Le bien i ∈ N d’un pays c ∈ C est produit à l’aide d’une fonction de production à rendements d’échelle constants

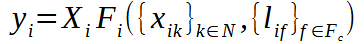
où y_i est la quantité totale de bien i produite, x_ik est un biens intermédiaires k, l_if est un facteur primaire de production f , et X_i la productivité exogène. Le producteur i choisit ces facteurs de production en minimisant ses coûts et fixe des prix égaux au coût marginal (cm_i) multiplié par un taux de marge p_i = µ_i × cm_i.

À l’équilibre, les marchés de tous les biens et facteurs s’équilibrent de sorte que

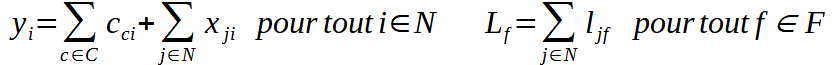
L’absorption (ou dépense nationale brute) pour le pays c, est le total des dépenses finales des résidents du pays :

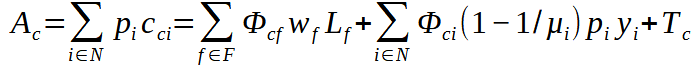
L’absorption coïncide avec le revenu national brut qui est le revenu des facteurs détenus par les résidents, ajusté des transferts internationaux.

Résultat théorique : la variation de bien-être est donnée par les variations de l’absorption qui combinent les changements dans les importations et les exportations de la façon suivante (l’indice c du pays considéré est omis) :

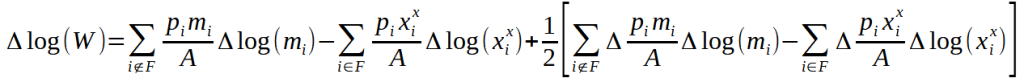
Illustration numérique. Si l’on note les importations d’énergie m_E et leur prix par p_E et si l’on supposons que la seule importation qui diminue est l’énergie, c’est-à-dire ∆ log mj = 0 pour tout j ≠ E. Supposons également que les autres exportations ne sont pas affectées ∆ log x^x_i= 0. Cette dernière hypothèse revient à une analyse d’équilibre partiel, sans substitution. Alors l’approximation de la variation de bien-être est

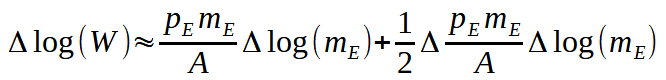
où le premier terme est proportionnel à la perte d’importation d’énergie pondérée par son poids dans l’absorption, et le second indique comment la part des importations d’énergie dans l’absorption varie en fonction de la substituabilité entre les facteurs impliquée par les élasticités et la structure input-output du modèle.

Considérons un cas extrême dans lequel toutes les importations d’énergie en provenance de Russie sont coupées (tout le gaz, le pétrole et le charbon) et l’Allemagne ne peut en remplacer aucune. Comme cela représente 30 % des importations énergétiques allemandes, on a ∆ log m_E = −30%. L’approximation du second ordre nécessite également une prédiction de l’évolution de la part de l’énergie dans l’absorption suite à l’embargo ∆(p_Em_E/A) . Un scénario extrême serait que cette part triple, passant alors de 2,5 % à 7,5 %, soit ∆(p_Em_E/A) = 5 %. Cela conduit alors à

∆ log W ≈ 2,5% × −30 % + (1/2) × 5% × −30% = −0,75% − 0,75% = −1,5%.

Ce scenario extrême (coupure de toutes les importations énergétiques russes, ne pas pouvoir les substituer et un triplement de la part des importations énergétiques) conduit à une réduction des dépenses totales allemandes de « seulement » 1,5%.

Contrairement à l’analyse menée dans le texte, cette illustration numérique ne tient pas compte de (i) l’endogénéité de p_E, (ii) d’éventuelles substitutions entre facteurs de production qui feraient alors intervenir les prix relatifs de ces intrants. Tous ces défauts sont « corrigés » dans l’approche de Baqaee et Farhi (2021) présentée dans la note.

Encadré 2 : Lien avec une analyse de la production à l’équilibre partiel (Bachmann et al (2022)).

Il est possible d’établir un lien entre production et énergie à partir de l’approximation d’une fonction de production CES, du type

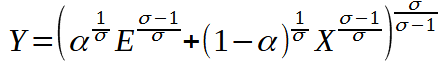
où α > 0 donne l’importance de l’énergie brune E dans la production Y et σ∈ [0, ∞) est l’élasticité de substitution entre l’énergie brune et les autres intrants X. On déduit

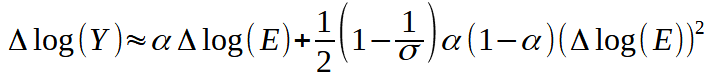
où il apparaît explicitement que la variation de la part des coûts de l’énergie dans la production ∆(p_EE/Y) dépend de l’élasticité de substitution σ. Comme les estimations de Bachmann et al (2022)  conduisent à α = 4%, on peut alors déduire les variations de PIB (Y) induites par une baisse des produits énergétiques (E) : pour σ=0,1, une baisse de 10% de intrants énergétiques implique alors une baisse de

∆log(Y) ≈ 4% × −10% – (1/2) × 9 × 3,84% × 100% = −0,18%,

alors que pour σ=0,01, on obtient ∆log(Y) ≈ -1,9%. Pour une baisse de 30% des intrants énergétiques, on obtient ∆log(Y) ≈ -1,57% σ=0,1 et ∆log(Y) ≈ -17% avec σ=0,01.

Le défaut majeur de cette approche est qu’elle néglige les possibilités qu’ont les entreprises de compenser les pertes liées aux variations de E par l’achat d’autres intrants X. Ces éventuelles substitutions feraient alors intervenir les prix relatifs des intrants, qui hélas ne sont pas endogènes dans cette modélisation à l’équilibre partiel. Tous ces défauts sont « corrigés » dans l’approche de Baqaee et Farhi (2021).

1. Bachmann, R, D Baqaee, C Bayer, M Kuhn, B Moll, A Peichl, K Pittel and M Schularick (2022), “What if? The Economic Effects for Germany of a Stop of Energy Imports from Russia”, ECONtribute Policy Brief 28/2022.
2. Nous remercions David Baqaee et Benjamin Moll pour le partage de leurs codes et leurs conseils.
3. Ceci est obtenu avec une élasticité de substitution de 0,1, valeur plus faible que celles de Labandeira et al (2017) et Auffhammer et al. (2018) qui indiquent des élasticités de court terme pour le gaz naturel de 0,18 et 0,2. Voir Labandeira et al. (2017) “A meta-analysis on the price elasticity of energy demand,” Energy Policy. Auffhammer et Rubin (2018) “Natural gas price elasticities and optimal cost recovery under consumer heterogeneity: Evidence from 300 million natural gas bills,” NBER.
4. Baqaee, D., and E. Farhi (2021), “Networks, barriers, and trade”. NBER Working Paper 26108.
5. La dépense nationale brute est retenue car (i) elle correspond au revenu national brut (voir encadré 1) et (ii) c’est elle que valorise le bien-être des ménages, pas le PIB.
6. La série utilisée est le revenu national domestique équivalent aux dépenses dans le modèle théorique, https://data.worldbank.org/indicator/NY.GNP.PCAP.PP.KD
7.  Nous retenons une élasticité de substitution égale à 0,1, proche des valeurs estimées reportées par Labandeira et al (2017) et Auffhammer et Rubin (2018), ou encore plus faible, i.e. égale à 0,00001, pour rendre compte d’un monde très rigide.
8. Schumacher et al. (2022) « Stopping Russian fossil fuel imports will help the green transition ». Sustainable Future Policy Lab : Opinions 2022-01.
9. De ces différences sectorielles, des différences entre les habitants de chaque pays pourraient être déduites. Cependant, le modèle ne permet pas d’aller plus loin, et limite l’analyse à un individu moyen par pays.