Le suivi d’une cohorte d’enfants permet de mettre en évidence l’influence sur le long terme que peuvent avoir les enseignants sur leurs élèves. Les travaux de Sarah Flèche à partir d’une cohorte britannique montrent que les enseignantes et enseignants du primaire ont un effet non seulement sur les notes de leurs élèves, mais aussi sur leurs compétences non-cognitives (par exemple l’estime de soi, la persévérance, ou encore les relations interpersonnelles). Cet effet s’observe à court terme sur les notes, mais s’estompe avec les années. Cependant, si l’effet sur les notes diminue au fil du temps, on continue à observer une influence des enseignants sur la réussite de leurs élèves à long terme, que ce soit à travers l’accès à l’université, l’insertion sur le marché du travail, leur santé mentale ou leurs comportements.
La capacité des enseignants à améliorer les performances cognitives de leurs élèves ne va pas nécessairement de pair avec leur capacité à améliorer la dimension non-cognitives. Les capacités à faire progresser les élèves dans l’un ou l’autre constituent deux compétences séparées. Ces compétences ne semblent pas s’acquérir principalement avec l’expérience, puisque l’âge, le nombre d’années d’exercice ou la confiance que les enseignants ont dans leurs pratiques ne semblent pas liées à la valeur ajoutée mesurée. En revanche, les pratiques pédagogiques mises en place par l’enseignant contribuent significativement à expliquer les différences de progressions entre élèves.
Cette note est une adaptation de l’article original : Sarah Flèche, « Teacher Quality, Test Scores and Non-Cognitive Skills : Evidence from Primary School Teachers in the UK », CEP Working Paper, N°1472, 2017.
Adaptation : Mathieu Perona et Sarah Flèche
Sarah Flèche, assistant professor Aix-Marseille School of Economics Chercheuse associée Observatoire du Bien-être du CepremapP, sarah.fleche@univ-amu.fr
Mathieu Perona, directeur exécutif de l’Observatoire du Bien-être du Cepremap, mathieu.perona@cepremap.org
Les horizons de l’influence des enseignants
Nous avons tous en mémoire des enseignantes ou des enseignants qui ont influencé notre destin scolaire. De fait, la recherche dans le domaine met en évidence deux effets, à première vue difficile à réconcilier1. D’une part, si on cherche à mesurer l’effet d’un enseignant sur les performances scolaires de ses élèves, le plus souvent par des tests standardisés, ces mesures font apparaître des impacts importants2. Mais ces effets des enseignants sur les performances scolaires de leurs élèves s’atténuent rapidement avec le temps. D’autre part, on constate que ces enseignants qui ont amélioré les performances scolaires de leurs élèves une année donnée ont une influence de long terme sur leur réussite future : leurs anciens élèves ont un meilleur taux d’accès à l’enseignement supérieur, à l’emploi et des revenus plus élevés3. Puisque cette influence ne se lit pas dans les résultats scolaires à long terme, cela peut signifier que ces enseignants, qui ont amélioré les performances scolaires de leurs élèves, ont transmis ou développé des compétences importantes pour leur succès futur, à l’université ou sur le marché du travail, mais qui ne sont pas en tant que telles évaluées par le système scolaire. La recherche identifie en effet un ensemble de compétences dites non-cognitives (voir encadré), par exemple la persévérance, la capacité à se motiver soi-même, l’estime de soi ou le contrôle de soi, qui constituent des atouts importants pour les études et la vie professionnelle4.
Ces constats ont des implications importantes pour la formation et l’évaluation des enseignants. Dès lors qu’on va au-delà de l’acquisition immédiate des connaissances, où l’effet individuel d’un enseignant s’estompe rapidement, il faut comprendre les relations qu’entretiennent les compétences cognitives et non-cognitives dans le temps et la façon dont les enseignants peuvent influencer ces compétences non-cognitives, tout aussi déterminantes pour la réussite future. Pour analyser ces relations, Sarah Flèche a utilisé des données de cohortes anglaises qui ont suivi des enfants de leur naissance à l’âge de 20 ans et qui ont permis de les observer dans leur environnement scolaire. Il devient ainsi possible d’identifier l’effet à court et long terme de leurs enseignants à la fois sur le développement de leurs compétences cognitives mais aussi de leurs capacités non-cognitives.
Ce travail a ainsi permis à l’auteur de mettre en évidence que :
- Les enseignants ont un impact sur les compétences non-cognitives de leurs élèves aussi bien que sur leurs compétences cognitives.
- L’acquisition de compétences cognitives et non-cognitives sont liées entre elles. Avoir un enseignant qui fait progresser la performance scolaire d’un élève améliore ses capacités non-cognitives dans le futur, et vice-versa.
- L’impact des enseignants sur les capacités non cognitives perdurent dans le temps et expliquent une part significative des différences observées à l’âge de 20 ans en termes d’éducation, d’insertion sur le marché du travail, de santé mentale et de comportements.
- La capacité d’un enseignant à améliorer les performances scolaires de ses élèves est assez indépendante de sa capacité à améliorer leurs compétences non-cognitives sur le court terme. Du point de vue de l’enseignement, ce sont donc deux enjeux pédagogiques différentes.
Méthode
Une vaste littérature cherche à estimer l’apport des enseignants à leurs élèves, le plus souvent en termes de résultats scolaires mais aussi, comme ici, sur des mesures d’insertion économique et sociale à plus long terme. Les résultats des élèves à une date donnée sont influencés par une multitude d’éléments individuels : leur origine sociale, le niveau de revenu de leur foyer, leur genre, leur travail antérieur (mesuré par leurs résultats les années précédentes), mais aussi collectifs, comme la composition de la classe. L’enjeu est de séparer l’influence de ces éléments de celle de l’enseignant (ou de l’établissement), que l’on désigne sous le terme de valeur ajoutée5. La valeur ajoutée d’un enseignant est ainsi l’écart entre les performances observées des élèves à la fin de l’année (ou au tout début de l’année suivante) et celles observées l’année précédente, en contrôlant pour toute l’information disponible sur les élèves et leur environnement scolaire entre ces deux périodes.
Effets à court et long terme des enseignants
Un impact sur la scolarité
L’impact le plus fort s’observe logiquement l’année même. En mathématiques, un enseignant meilleur en termes de valeurs ajoutée que 85 % de ses collègues augmentera la note de ses élèves de 0,5 points (sur 20) par rapport à un enseignant moyen. C’est ce que nous représentons sur la figure 1. Nous supposons qu’un élève a eu une année donnée un enseignant dont la valeur ajoutée est un écart-type au-dessus de la moyenne de ses collègues, c’est-à-dire meilleure de 85 % d’entre eux. Nous calculons ensuite la différence entre le score de cet élève et celui d’une camarade issue d’une famille similaire, qui aurait eu un enseignant dont la valeur ajoutée est à la moyenne.
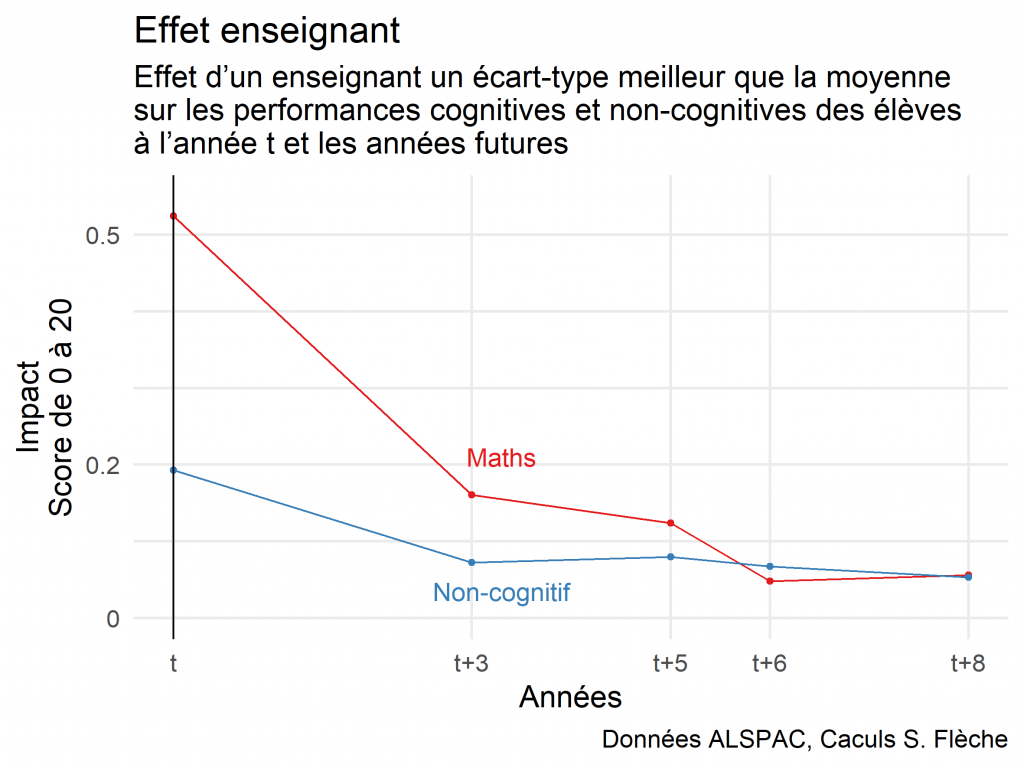
Figure 1 : Impact d’un enseignant jusqu’à 8 ans après avoir quitté sa classe.
L’ampleur des effets ainsi calculés découle en partie du mode de comparaison que nous avons adopté. Ainsi, l’écart de valeurs ajoutées entre un enseignant est ramené sur une échelle de zéro à vingt pour faciliter les comparaisons. Il faut également noter qu’il s’agit de l’impact moyen sur l’ensemble des élèves de cet enseignant : un impact d’un demi-point en moyenne signifie une capacité soit à augmenter les résultats de l’ensemble de la classe6, soit à augmenter très nettement les résultats d’une partie de la classe sans dégrader ceux du reste.
À plus long terme, l’effet d’un enseignant sur les performances en mathématiques s’atténue avec le temps. Si nous comparons dans le temps un élève qui aurait eu une année donnée un enseignant meilleur d’un écart-type par rapport à ses collègues avec un élève qui aurait eu un enseignant moyen, le premier aurait trois ans après un score supérieur en mathématiques de 0,16 points. Huit ans plus tard, on constate encore un écart de 0,05 points : faible en valeur absolue, mais cela signifie qu’à la sortie du collège, l’enseignant de primaire continue à avoir un effet sur les notes de ses anciens élèves. Il importe ici de souligner que cette persistance, y compris lorsqu’elle est mesurée par des tests qui ne comptent ni dans les bulletins scolaires des élèves ni dans l’évaluation des enseignants, indique que la valeur ajoutée mesurée en mathématiques ne repose pas essentiellement sur une préparation au test, mais bien sur un développement des compétences mathématiques de fond.
Dans le domaine non-cognitif, l’effet immédiat est plus faible, de 0,2 points sur 20, mais persiste plus fortement dans le temps. Huit ans plus tard, l’effet d’avoir eu enseignant plus performant dans sa capacité à améliorer les capacités non-cognitives de ses élèves reste de 0,05 points, soit un effet équivalent à 25 % de son effet initial. Rappelons que ce score non-cognitif se fonde sur les réponses des parents. L’effet de l’enseignant dans ce domaine est donc suffisamment fort pour être remarqué par les parents, y compris plusieurs années après.
Dans son travail, Sarah Flèche met aussi en évidence que les effets des enseignants se cumulent dans le temps. En d’autres termes, les impacts des enseignants s’additionnent, qu’il s’agisse des mathématiques ou du comportement. Cela confirme que cette mesure de valeur ajoutée correspond bien à l’acquisition de compétences fondamentales, et non d’une avance temporaire sur les autres élèves du même âge.
Enfin, l’expérimentation montre que les progrès se renforcent mutuellement. Ainsi, les élèves d’un enseignant à forte valeur ajoutée en mathématiques voient leurs scores non-cognitifs progresser l’année suivante plus que ceux des élèves d’un enseignant à moins forte valeur ajoutée en mathématiques, et inversement.
Des effets à long terme
Bien qu’on leur accorde beaucoup d’importance sur le moment, les notes en mathématiques ne constituent pas un objectif en soi. Elles n’intéressent que dans la mesure où elles indiquent l’acquisition de compétences qui seront utiles dans la suite du parcours des élèves.
Nous venons de voir plus haut que l’impact mesurable d’un enseignant sur les performances cognitives et non-cognitives d’un élève donné s’atténue avec le temps. Pourtant, plusieurs études ont aussi mis en évidence des effets à beaucoup plus long terme, en particulier sur l’accès aux formations supérieures et à l’emploi. Ici, le suivi des élèves permet de constater que ce que les études précédentes avaient observé sur des échantillons séparés s’observe aussi lorsqu’on suit les mêmes élèves : on mesure à la fois une atténuation de l’effet sur les scores et un impact significatif sur la situation scolaire et sociale de ces enfants devenus de jeunes adultes.
Le tableau 1 restitue les impacts mesurables à 18 ou 20 ans du fait d’avoir eu à 8 ou 11 ans un enseignant dont la valeur ajoutée est supérieure d’un écart-type à la moyenne de ses collègues sur une sélection d’indicateurs : le fait de finir le lycée, l’accès à l’université, le choix d’une filière scientifique, le revenu espéré à 40 ans, un score standardisé de santé mentale7, le fait de boire de l’alcool au moins une fois par semaine, le fait d’avoir déjà fumé et le fait d’avoir déjà fait un don à une association caritative.
| Aspect | Référence | Maths | Non-cog |
|---|---|---|---|
| Lycée | 74 % | +2,6 (+3,5 %) | +2,6 (+3,5 %) |
| Université | 45 % | +3,4 (+7,5 %) | +3,6 (+8,0 %) |
| Études scientifiques | 17 % | +1,3 (+7,5 %) | +0,7 (+4,0 %) |
| Revenus espérés | 26 500 £ | +384 ( +1,4 %) | -285 (-1,1 %) |
| Santé mentale | 19 | +0,19 (+1,0 %) | +0,23 (+1,2 %) |
| Alcool | 17 % | -0,5 (-29 %) | -0,7 (-41 %) |
| Tabac | 46 % | -0,1 (-0,2 %) | -1,7 (-3,7 %) |
| Don | 50 % | +0,6 (+1,2 %) | +2,3 (+4,6 %) |
Lecture : Au sein de la cohorte, 45 % des élèves ont accédé à l’université. Un enseignant dont la valeur ajoutée en mathématiques est un écart-type au-dessus de la moyenne augmente de 3,6 points de pourcentage la probabilité que ses élèves aillent à l’université (une progression de 7,5 %).
Les effets en italiques et en gris ne sont pas statistiquement significatifs.
Ainsi, avoir été dans la classe d’un enseignant ou d’une enseignante plus performante sur les mathématiques, comme défini précédemment, augmente de 2,6 points de pourcentage la probabilité de finir le lycée, et et de 3,4 points celle d’aller à l’université. Dans la cohorte concernés, 45 % des enfants suivis sont allés à l’université. Une augmentation de 3,4 points de la probabilité d’accès correspond donc à une augmentation de 7,5 % de la probabilité d’accès au supérieur, simplement du fait d’un enseignant de primaire particulièrement efficace. L’impact de long terme de la valeur ajoutée non-cognitive est très similaire à celui des mathématiques, et s’ajoute à ce dernier. Ainsi un élève ayant eu (pas forcément la même année) un enseignant performant dans chaque domaine a une probabilité 15 % plus élevée d’accéder à l’université que ses camarades ayant eu des enseignants moyens.
Ces chiffres démontrent une remarquable persistance de l’influence des enseignants du primaire non seulement sur la destinée scolaire de leurs anciens élèves, mais aussi sur un ensemble plus large d’attitudes et de comportements essentiels. La mise en regard des deux constats suggère ainsi que l’effet des enseignants à long terme passe par d’autres biais que ceux mesurés par les notes, ici le score en mathématiques, et par l’indicateur non-cognitif.
Enseigner, une question de méthode ?
Face à ces résultats, on se pose naturellement la question de savoir ce qui explique les différences de valeur ajoutée entre les enseignants. Si les meilleures performances reposent sur des pratiques d’enseignement, celles-ci peuvent être enseignées et adoptées par les collègues.
Des compétences séparées
Nous avons mentionné plus haut qu’il existait un effet croisé dans l’acquisition : les élèves qui progressent en mathématiques grâce à un bon enseignant une année voient leurs scores comportementaux augmenter aussi les années suivantes. Est-ce à dire qu’il y a au fond simplement de bons enseignants, qui font progresser leurs élèves dans les deux domaines, et de moins bons enseignants ? En d’autre termes, est-ce qu’on observe aussi un effet croisé dans la transmission ?
En pratique cependant, les deux compétences apparaissent bien distinctes. Sur la figure 2, chaque point est un enseignant (certains sont observés deux ou trois fois), positionné par la valeur ajoutée dans chaque dimension. On constate que la corrélation entre les deux dimensions est faible : la droite bleue est proche de zéro et la relation qu’elle représente n’est pas significative. Ainsi, un enseignant à forte valeur ajoutée en mathématiques n’augmentera pas nécessairement les capacités non-cognitives de ses élèves et vice versa.
On constate également qu’il y a peu d’enseignants qui seraient très mauvais dans les deux dimensions (le coin en bas à gauche du graphique), et peu de super-enseignants qui seraient très performants dans les deux dimensions (partie en haut à droite). Ce résultat suggère ainsi que les capacités à faire progresser les élèves mobilisent des pratiques ou des attitudes différentes selon les domaines.
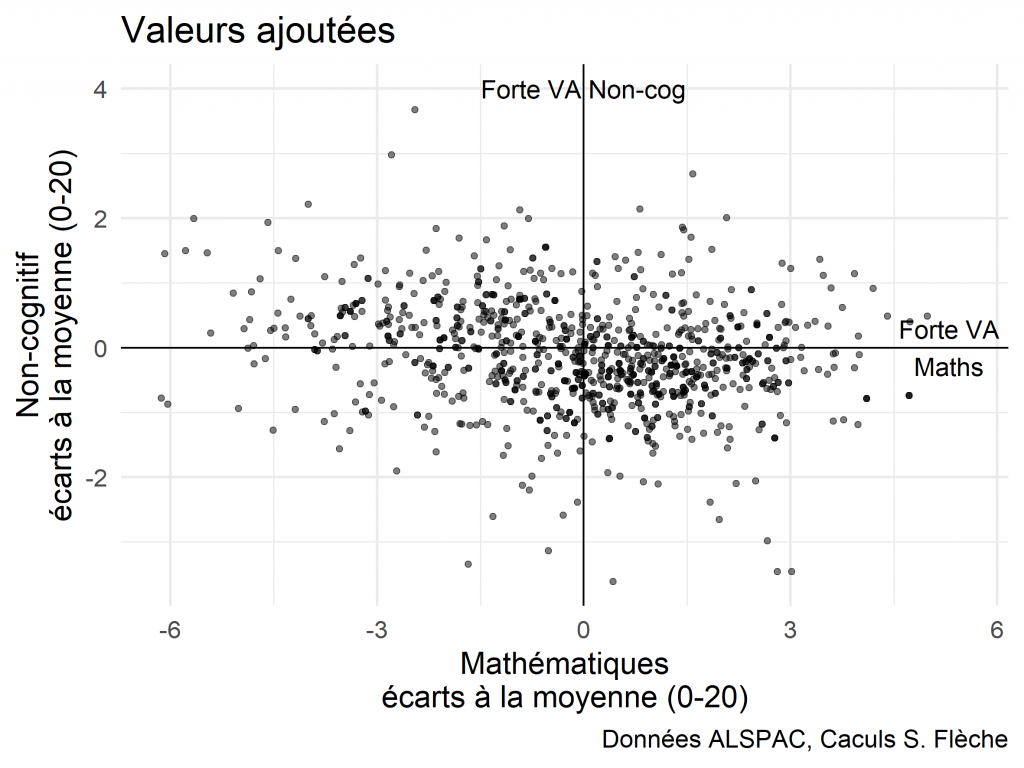
Figure 2 : Valeurs ajoutées, ramenées à une échelle de 0 à 20. Chaque point correspond à une observation (enseignant, année). Les points sont semi-transparents afin de mettre en évidence les endroits où plusieurs observations se superposent.
Une question de pratiques
Est-il possible de dresser le portrait d’un enseignant ou d’une enseignante à haute valeur ajoutée ? La base de données utilisée disposant de nombreuses information sur les enseignants, il est possible d’estimer les relations entre un certain nombre de caractéristiques et la valeur ajoutée8. La conclusion est d’abord négative : le nombre d’années d’enseignement (totales ou dans l’école actuelle), le temps passé à enseigner les mathématiques et même le score de santé mentale de l’enseignant n’ont pas de relation significative avec son niveau en valeur ajoutée. De même, le niveau d’estime de soi ou le niveau de confiance à l’égard de ses propres pratiques d’enseignement n’apportent pas d’information sur la valeur ajoutée mesurée. En termes de genre, les femmes ont un niveau de valeur ajoutée moyen un peu supérieur à celui de leurs collègues masculins dans le domaine non-cognitif, et équivalent en ce qui concerne les mathématiques.
De fait, l’élément observable le plus déterminant semble être les méthodes d’enseignement. Une analyse en composantes principales montre qu’en combinant plusieurs pratiques d’enseignement, telles que des interactions fréquentes avec la classe, une valorisation des élèves ayant bien réalisé un exercice, ainsi que la mise en place de travail de groupe, toutes choses égales par ailleurs (c’est-à-dire à caractéristiques de l’enseignant similaires), ces pratiques sont associées positivement avec la valeur ajoutée d’un enseignant à la fois en mathématiques comme dans le domaine non-cognitif.
Bibliographie
Article source
Sarah Flèche, « Teacher Quality, Test Scores and Non-Cognitive Skills : Evidence from Primary School Teachers in the UK », CEP Working Paper, N°1472, 2017.
Articles cités
Chetty, R., J. N. Friedman, and J.E. Rockoff. 2014a. “Measuring the Impacts of Teachers I: Evaluating Bias in Teacher Value-Added Estimates”. American Economic Review 104(9): 2593-632.
Chetty, R., J. N. Friedman, and J.E. Rockoff. 2014b. “Measuring the Impacts of Teachers II: Teacher Value-Added and Student Outcomes in Adulthood”. American Economic Review 104(9): 2633-79.
Heckman, J.J., J. Stixrud, and S. Urzua. 2006. “The Effects of Cognitive and Noncognitive Abilities on Labor Market Outcomes and Social Behavior”. Journal of Labor Economics 24(3): 411-82.
Encadré 1 : les données
L’étude repose sur l’Avon Longitudinal Study of Parents and Children(ASLPAC). Cette cohorte regroupe 70% des enfants nés entre mars 1991 et février 1993 à Bristol (Royaume-Uni) et dans les environs (comté d’Avon). Les enfants sont suivis chaque année, de leur naissance jusqu’ à l’âge de 20 ans. Lorsque ces enfants ont atteint 8 et 11 ans, un questionnaire a été administré à leurs enseignants. Ces âges correspondent respectivement à la troisième et dernière année du primaire au Royaume-Uni (« year 3 » and « year 6 »), au CE1 et CM2 en France. On dispose ainsi d’informations très détaillées sur les enfants, leur environnement familial et socio-économique, ainsi que sur leurs milieux scolaires. L’échantillon couvre 1054 enseignants répartis dans 476 écoles.
Les compétences en mathématiques de tous les élèves britanniques sont évaluées par des tests nationaux aux âges de 7, 11, 14 et 16 ans. (Key stages 1, 2, 3, and 4). Pour les besoins de l’enquête, les enfants de la cohortes ont participé à deux tests complémentaires, à 9 et 11 ans. Ne comptant ni dans les bulletins des élèves ni dans les évaluations des enseignants, ces deux tests complémentaires fournissent une mesure qui n’est pas soumise à la pression aux résultats. Sur le volet non-cognitif, les parents remplissent le Strength and Difficulties Questionnaire, dont les réponses sont agrégées sous la formes d’indicateurs synthétiques. Ce questionnaire fournit de 5 à 16 ans une mesure cohérente. Cette mesure est dissociée de l’institution scolaire, puisque n’incluant pas les retards, absences et sanctions, même si on observe une forte relation entre le résultat du questionnaire et ce type d’événements.
À partir de 18 ans, l’étude comprend aussi des informations sur le niveau de diplôme atteint, l’insertion sur le marché du travail, la santé, le bien-être subjectif, comportements sociaux et aspirations. Le bien-être subjectif est plus particulièrement mesuré par le Short Moods and Feelings Questionnaire, qui comprend 33 questions et est couramment utilisé pour repérer les risques dépressifs. Les questionnaires relèvent également chez les jeunes adultes la consommation de tabac et d’alcool ainsi que la participation à des actions caritatives.
Encadré 2 : les compétences non-cognitives
Pour évaluer les compétences non-cognitives des enfants, ce travail mobilise le Strength and Difficulties Questionnaire, destiné à la détection de problèmes psychologiques (comportement, hyperactivité, inattention, problèmes relationnels, difficultés de gestion des émotions). Largement employé dans les recherches en sciences sociales, quatre rubriques de ce questionnaire sont utilisées avec cinq questions chacune : problèmes émotionnels (enfant facilement effrayé, souvent triste ou anxieux), relation avec les autres enfants (a-t-il des amis ? est-il victime de brimades ou de harcèlement ?), comportement (crises de colère, tricheries ou mensonges répétés), hyperactivité et inattention (réfléchit-il avant d’agir ? a-t-il du mal à se concentrer sur une activité ?). Chaque question porte trois modalités de réponse de zéro à deux, l’ensemble fournissant des scores de 0 à 20 sur les comportements « intérieurs » (« internalizing SDQ, émotions et relation avec les autres) et sur les comportements « extérieurs » (« externalizing SDQ, comportement et hyperactivité).
Afin de faciliter la comparaison avec les résultats des tests de mathématiques, ce travail a construit un score non-cognitif comme la moyenne des deux scores ci-dessus. L’ordre a été inversé, de manière à ce qu’à l’image de la notation en mathématiques, zéro indique le cas le plus problématique et 20 le cas le plus favorable.
- Nous donnons ici une vue d’ensemble de la littérature utile pour comprendre les enjeux des résultats que nous présentons. Nous n’incluons pas dans le texte l’ensemble des références, qui sont mentionnées dans l’article dont cette note est une adaptation (voir Flèche, 2017).
- Chetty et al., 2014a.
- Chetty et al., 2014b.
- Heckman et al., 2006.
- En France, le Ministère de l’Éducation Nationale procède ainsi pour calculer des valeurs ajoutées au niveau des lycées : https://www.education.gouv.fr/methodologie-des-indicateurs-de-resultats-des-lycees-11948.
- Soit pour une classe de 28 élèves, une augmentation totale de 14 points (=28*0,05 points).
- Voir l’Encadré 1 sur les métriques utilisées.
- Table A.17 de l’article.